最近开始准备找实习,各大公司的题自然是不可错过,今天看到一道抛硬币方面的概率题,找了下看到网上的答案几乎都是错的,这里给出自己的推理。
题目如下:
假定抛出的硬币落地之后正反两面出现的概率分别是 1/2。那么抛 10 次和 100 次硬币(分别称为 T10 和 T100)相比,以下说法正确的是:
A. T100 出现一半的正面比 T10 出现一半正面的概率更大
B. T100 前 3 次都是正面的概率比 T10 前 3 次都是正面的可能性大
C. T100 正面次数的方差小于 T10 出现正面次数的方差
D. T100 出现正面的比例比 T10 出现正面的比例在(0.45,0.55)区间中的可能性更大。
抛的次数越多,最后出现正面的次数自然也就越接近平均数,即出现正面的比例越接近0.5,这个倒很好理解,所以网上很多答案为C. 理由是100次的方差越小嘛,而出现正面的比例应该都是一样的,因为每次抛出现正面的概率都是0.5…
以下先从直觉上推翻以上谬论,「出现正面的比例越接近0.5」这个我想大家没有异议,那么既然出现正面的比例越接近0.5,也就是说出现正面的次数越集中在抛的总数的一半,从反面来说也就是正面次数在靠近0或者最大值的比例越少,因此也就意味着方差越大!,而不是方差越小!我们直觉上的「方差」和这个题目中的「方差」可是有出入的。由于抛的次数越多,正面次数越靠近中央,故选D。以下从数学角度给出相对严格的分析。
显然抛硬币这个过程是一个独立的二项分布,上过高中数学的都知道二项分布 $X \sim B(n,p).$ 的均值为np, 方差为npq, 因此n越大方差越大。对于D,分析起来相对麻烦一丁点,在np >= 5时,可以采用正态分布来近似。由于D中问的是出现正面的比例,而不是出现正面的次数,即由原来的 $X \sim B(n,p).$ 转变为现在的$\frac{1}{n} \cdot X$,这里的n对于X来说相当于常量,故「出现正面的次数的比例」可等价于变量Y.
$$E(Y) = \frac{1}{n} \cdot E(X) = p$$ $$D(Y) = \frac{1}{n^2} \cdot D(Y) = \frac{1}{n} \cdot p(1-p)$$
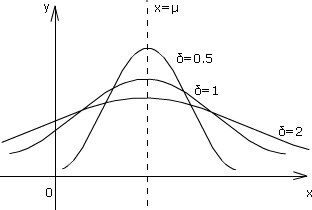
从上式可以看到 $n$ 越大,其方差越小,也就是在(0.45, 0.55)区间中的可能性越大。 方差越小的概率密度函数越「瘦削」——几乎全部集中在均值附近,因此答案为D.
另一道有意思的概率题——有道概率题:一个有趣的抛硬币问题 - atyuwen